- Dozent*in: Marc Fischlin
- Dozent*in: Patrick Harasser
- Dozent*in: Christian Janson
- Dozent*in: Felix Rohrbach
Lehrinhalte:
- Datenstrukturen: Array, Listen, Binäre
Suchbäume, B-Bäume, Graphenräprentationen, Hashtabellen, Heaps
- Algorithmen: Sortieralgorithmen, Stringmatching, Traversieren,
Einfügen, Suchen und Löschen bei bestimmten Datenstrukturen, Kürzeste
Wege Suche, Minimal Spannende Bäume
- Asymptotische Komplexität
- Algorithmisches Strategien: Divide-and-Conquer, Dynamische Programmierung, Brute-Force, Greedy, Backtracking, Metaheuristiken
- Dozent*in: Marc Fischlin
- Dozent*in: Patrick Harasser
- Dozent*in: Christian Janson
- Dozent*in: Felix Rohrbach
Syntax und Semantik der Aussagenlogik, funktionale Vollständigkeit und Normalformen, Kompaktheitssatz der Aussagenlogik, vollständige Beweiskalküle: Resolution und ein Sequenzenkalkül;
Syntax und Semantik der Logik erster Stufe, Strukturen und Belegungen, Normalformen und Skolemisierung, der Satz von Herbrand und der Kompaktheitsstaz der Logik erster Stufe, vollständige Beweiskalküle: (Grundinstanzen-)Resolution und ein Sequenzenkalkül,
Gödelscher Vollständigkeitssatz, Unentscheidbarkeit der Logik erster Stufe;
optional: Exkurse zu Ausdrucksstärke und model checking
Literatur:
Burris: Logic for Mathematics and Computer Science
Schöning: Logik für Informatiker
Boolos, Burgess, Jeffrey: Computability and Logic
Skript (2 Teile, elektronisch unter www.mathematik.tu-darmstadt.de/~otto)
- Dozent*in: Ulrik Buchholtz
- Dozent*in: Kord Eickmeyer
- Dozent*in: Jonathan Weinberger
Moodlekurs zur Lehrveranstaltung Informationsmanagement, ehem. Einführung in Data and Knowledge Engineering (20-00-0015) sowie zu Allgemeine Informatik III.
- Dozent*in: Thomas Arnold
- Dozent*in: Carsten Binnig
- Dozent*in: Nils Boeschen
- Dozent*in: Iryna Gurevych
Lehrinhalte:
- Analysis in R: Potenzreihen, Elementarfunktionen, Differenzial-
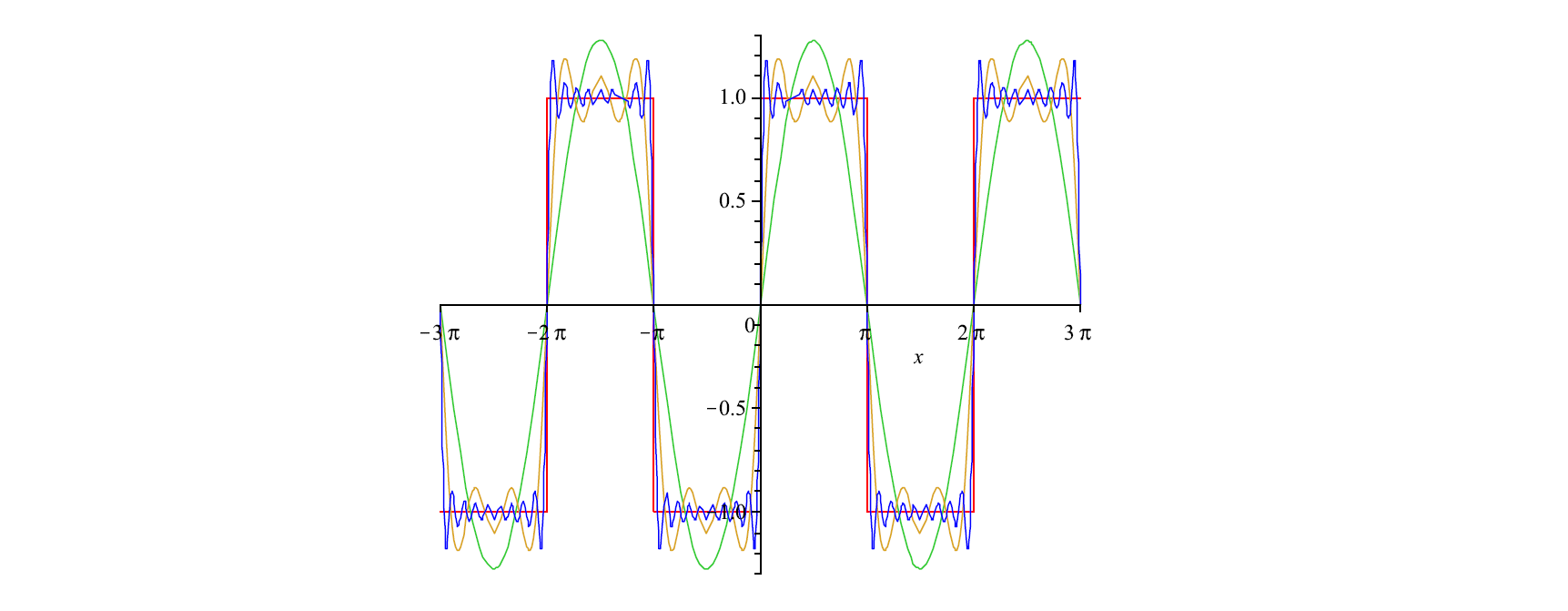
und Integralrechnung, Satz von Taylor, Extremwerte, Fourierreihen
- Analysis mehrer Veränderlicher: Stetigkeit, partielle und totale Differenzierbarkeit, Extremwerte, Kurven
- Gewöhnliche Differentialgleichungen: Systeme linearer DGLen, Satz von Picard-Lindelöf
- Allgemeine Algebra: Algebren und Unteralgebren, Homomorphismen, Quotienten
- Dozent*in: Ulrik Buchholtz
- Dozent*in: Sandra Lang
- Dozent*in: Anne-Therese Rauls
- Dozent*in: Thomas Streicher
- Dozent*in: Tobias Hamann
Der Treffpunkt Mathematik ist ein freiwilliges
Zusatzangebot des Fachbereiches Mathematik, das als Ergänzung zu den
grundlegenden Mathematikvorlesungen in den ersten Semestern gedacht ist.
Er besteht seit dem WS
2011/2012. Die
vorlesungsbegleitenden Veranstaltungen werden durch einen Klausurvorbereitungskurs in der vorlesungsfreien Zeit ergänzt.
- Dozent*in: Gabriel Teschner
